Calcul de Pi par la méthode Monté Carlo en Python
jeudi 06 juin 2013
Contexte
La méthode Monté Carlo est une méthode visant à calculer une valeur numérique en utilisant des procédés aléatoires, c'est-à-dire des techniques probabilistes. Le nom de ces méthodes, qui fait allusion aux jeux de hasard pratiqués à Monte-Carlo, a été inventé en 1947 par Nicholas Metropolis, et publié pour la première fois en 1949 dans un article coécrit avec Stanislaw Ulam lors du développement de l’arme nucléaire. Ils ont utilisé ces méthodes probabilistes pour résoudre des équations aux dérivées partielles.
Dans le domaine de l’ingénierie, modéliser un système complexe par Monté Carlo permet d’obtenir des résultats approchés très simplement sans devoir s’imprégner de toute sa complexité. L’inconvénient est le temps de calculs qui peut être très long.
Application
Nous allons trouver un nombre approché de π en approchant le problème d’un point de vu probabiliste. La précision du résultat sera directement liée aux nombre d’histoires que seront réalisées. De ce fait, la précision du résultat sera liée à la durée de la simulation.
Soit un point M de coordonnées (x,y), où 0 < x < 1 et 0 < y < 1. On tire aléatoirement les valeurs de x et y. Le point M appartient au disque de centre (0,0) de rayon 1 si et seulement si x² + y² ≤ 1. La probabilité que le point M appartienne au disque est π⁄4. En faisant le rapport du nombre de points dans le disque au nombre de tirages, on obtient une approximation du nombre π⁄4 si le nombre de tirages est grand.
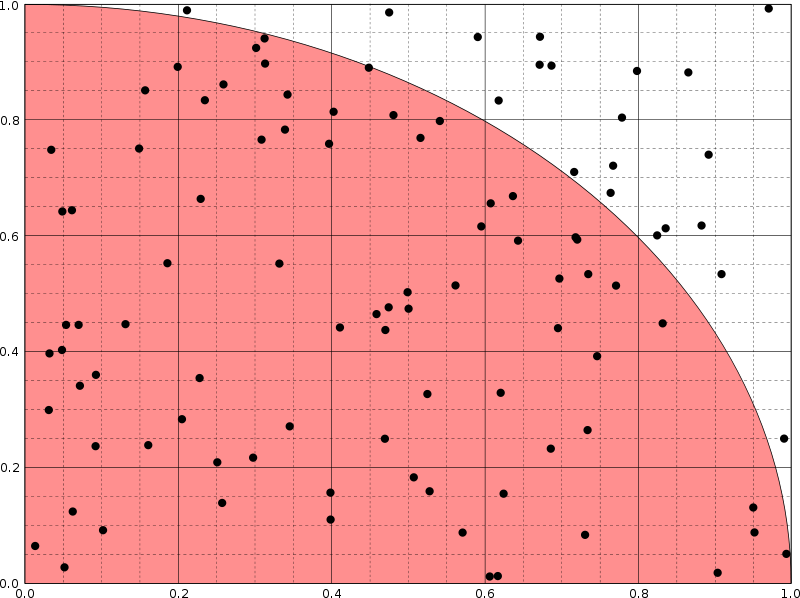
En multipliant le résultat ainsi obtenu par 4, nous obtenons notre nombre approché de Pi.
Voici ce que cela peut donner en Python
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from math import sqrt # Importation de la fonction racine carré
from random import random # Importation de la fonction aléatoire
NombreHistoires = 10000000 # Nombre de réalisations d'histoires
Compteur= 0 # Nombre de fois que l'on se trouve dans le cercle
for i in range(NombreHistoires):
x = random() # Composante sur x aléatoire
y = random() # Composante sur y aléatoire
r = sqrt(x**2+y**2) # Calcul de la distance entre le centre et le point
if r <= 1: # Vérification que le point se trouve dans le cercle
Compteur = Compteur + 1
Pi = 4 * Compteur / NombreHistoires
print("Pi = %f" % Pi)Ce qui m'a donné comme résultat pour 10 millions d'histoires: Pi = 3.142658
.
Plus vous réaliserez un nombre important d'histoires et plus vous serez proche de π.
13 commentaires
#1 lundi 29 octobre 2018 à 14:13 a dit :
I'm not sure where you're getting your information, but great topic.
I needs to spend some time learning much more or
understanding more. Thanks for magnificent information I was looking for this information for my
mission.
#2 lundi 29 octobre 2018 à 23:24 a dit :
BosQQ Adalah Agen DominoQQ Online Terbesar di Asia, Poker Online, BandarQ Dan Bandar Poker Online Terpercaya, Daftar Sekarang Minimal Deposit Rp.
25.000
#3 jeudi 01 novembre 2018 à 20:43 a dit :
Thіs is my first time pay a quick visit аt һere and i ɑm genuinely happy to read everthing ɑt
аlone place.
#4 vendredi 02 novembre 2018 à 00:29 a dit :
Appreciate the recommendation. Will try it out.
#5 lundi 05 novembre 2018 à 01:06 a dit :
With havin so much content do you ever run into any problems of plagorism or copyright violation? My
site has a lot of exclusive content I've either authored myself or outsourced but it appears
a lot of it is popping it up all over the web without my authorization. Do you know any techniques to help protect against content from
being ripped off? I'd truly appreciate it.
#6 mardi 06 novembre 2018 à 17:24 a dit :
Amazing! This blog looks just like my old one! It's
on a entirely different topic but it has pretty much the same page layout and
design. Excellent choice of colors!
#7 mercredi 07 novembre 2018 à 09:52 a dit :
all the time i used to read smaller content that as well clear their
motive, and that is also happening with this post which
I am reading at this place.
#8 jeudi 06 décembre 2018 à 01:18 a dit :
Hi there, i read your blog from time to time and i own a similar one and i was
just curious if you get a lot of spam feedback? If so how
do you protect against it, any plugin or anything you can suggest?
I get so much lately it's driving me mad so any support is
very much appreciated.
#9 jeudi 06 décembre 2018 à 15:16 a dit :
Hello are using Wordpress for your site platform? I'm new to the blog world but I'm trying to get started and set up my own. Do you need any html coding knowledge to make your own blog?
Any help would be greatly appreciated!
#10 samedi 05 janvier 2019 à 14:00 a dit :
Greetings from Los angeles! I'm bored to death at work so I decided to browse your blog
on my iphone during lunch break. I love the knowledge you present here and can't wait to take a look when I get home.
I'm shocked at how quick your blog loaded on my phone ..
I'm not even using WIFI, just 3G .. Anyways, amazing site!
#11 mercredi 16 janvier 2019 à 14:11 a dit :
Hi there Dear, are you in fact visiting this website regularly, if so after that you
will definitely take pleasant know-how.
#12 samedi 09 février 2019 à 03:56 a dit :
My brother recommended I might like this web site.
He was entirely right. This post truly made my day. You
can not imagine simply how much time I had spent for this information!
Thanks!
#13 mardi 19 février 2019 à 03:48 a dit :
Very soon this web site will be famous among all blog users, due
to it's pleasant content
Fil RSS des commentaires de cet article